Excel challenge 1, Combinations, combinations
The challenge
This challenge was first posted on Daily Dose Of Excel. In my newsletter for May 2019 I showed you a trick to get all possible combinations of two lists. This is a related problem.
Suppose I have 10 ballot tickets. My job is to draw 5 random tickets from that set of 10 repeatedly until I have drawn all possible combinations:
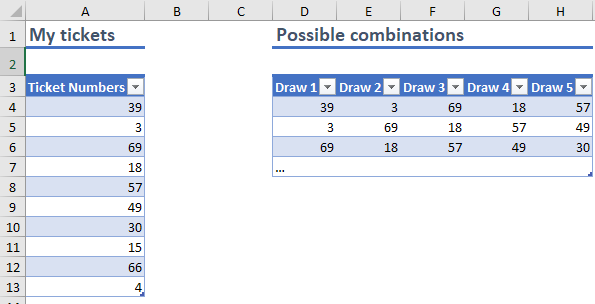
The challenge I would like to give you all: Please use any technique in Excel to list all possible unique combinations of ticket numbers drawn this way.
Note that the order in which the tickets are drawn makes no difference and that each number can only be drawn once per set of 5. This means that a draw of (1, 2, 3, 4, 5) is considered the same as (5, 4, 3, 2, 1) or (2, 1, 3, 4, 5). What's in it for you? The 5 best submissions will receive:
- Eternal fame
- A free one-year license for my RefTreeAnalyser utility
Solutions
I received a total of 9 submissions for this challenge (thanks everyone!). It is quite a lot of work to describe them all in full detail here, so I'll group them by technology used. I'll also announce a group winner below.
Of course Excel has a function with which you can calculate the total number of unique combinations:
=COMBIN(10,5)
which yields 252. That means that if a solution does not have 252 possible combinations the solution is (alas!) wrong.
Formula solutions
Three people submitted a solution involving formulas in Excel. Dan Mayoh, Doug Jenkins and Richard Jubber. Two of them were correct and both used a very similar approach to get the correct combinations.
Download the two correct formula solutions
Group winner
The best formula solution was provided by Dan Mayoh. Dan went out of his way to deliver a nicely structured and formatted workbook which is designed in such a way that you can add more draws if you like and even change the number of available tickets. You do have to do some formula copying if you want more than the default numbers, but the plumbing is there.
Here is a screen-shot:
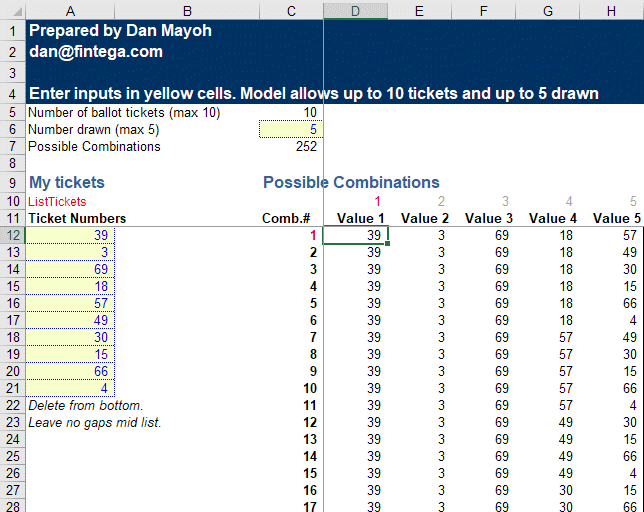
I plan to have an explanation here, which I'll ask Dan to write :-)
Runner-up in this category is Doug Jenkins. Doug also posted a VBA solution for which he received some bonus points.
VBA Solutions
Four people submitted a solution using VBA: Harald Staff, Garys Student, Doug Jenkins and Gerard Oudewaal. All four of them used very similar techniques.
Group winner
The best VBA solution was provided by Harald Staff. Harald also enables us to change the ticket numbers, though he did not go as far as Dan so we cannot add more draws if we like or change the number of available tickets.
Runner-up in this category is Garys Student (I already made Doug runner up in the formula category, can't win twice!) and a nice third place for Gerard Oudewaal.
PowerQuery solutions
Jeff Weir and Jonathan Cooper both posted a solution based on PowerQuery, both using a similar technique using my aforementioned newsletter article as its basis.
Download the PowerQuery solutionsGroup winner
I call it a draw. Jeff uses less queries in his solution, but Jonathan's final query involves less steps.
And the overall winner is....
Dan Mayoh !
I've decided to provide all correct solutions with a free license for my RefTreeAnalyser utility. Congratulations to the winners, you'll receive your license as soon as possible.
How to calculate the number of combinations
I asked the participants if they might explain the solution method and I particularly liked this one from Harald Staff:
"Many years ago, I worked at a quiz show. One of the challenges was to get seven questions, discard two, and answer the remaining five correctly. The producer asked me how many possible combinations there might be. I made this illustration for her:
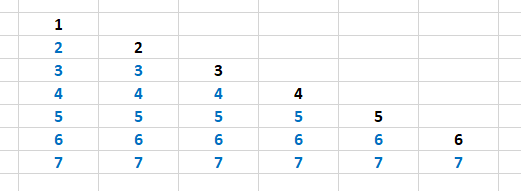
showing: 1 can only be combined with 2,3,4,5,6,7. 2 can be then only be combined with 3,4,5,6,7 (1 has already been used with all other numbers so no longer can be drawn). 3 can be combined with 4,5,6,7 (as now 1 and 2 are off the table). And so on, summing up to 6+5+4+3+2+1=21 combinations. Your combinations challenge was very similar. Unique items only once each, and the order of items does not matter. ABC and ACB are the same.
My approach was also similar; work the table from the top and downwards. To simplify the technique, here are five unique items, and let us see how to find all the unique collections of three unique items.
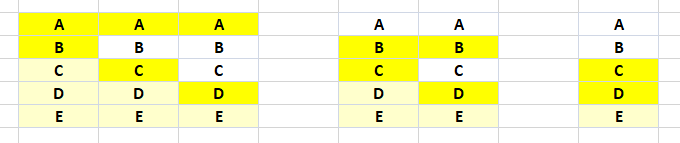
I use three loops for this. The outer loop controls the first item, A at the beginning, the second loop controls the middle item, B at the beginning, and the inner loop does the possible third items C, D and E. So, we start on top, AB is combined with C, D and E. Now AB is done, we move to AC, which is combined with D and E. Finally AD is combined with E. Now we are done with A, the top item is now B. BC is combined with D and E, and BD is combined with E. Done with B, our final starting point is CD, which can only have E. Best wishes Harald"

Comments