Excel challenge 1, Combinations, combinations
The challenge
This challenge was first posted on
Daily Dose Of Excel. In my
newsletter for May 2019 I showed you a trick to get all possible
combinations of two lists. This is a related problem.
Suppose I have 10 ballot tickets. My job is to draw 5 random tickets
from that set of 10 repeatedly until I have drawn all possible
combinations:
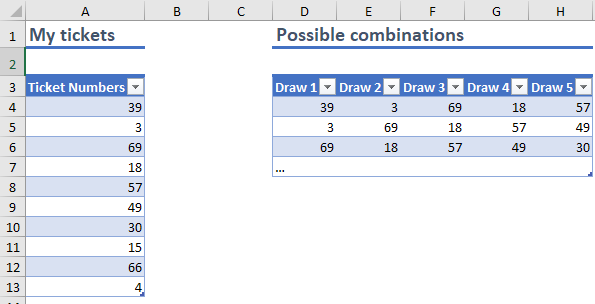
The challenge I would like to give you all: Please use any technique
in Excel to list all possible unique combinations of ticket numbers
drawn this way.
Note that the order in which the tickets are drawn makes no
difference and that each number can only be drawn once per set of 5.
This means that a draw of (1, 2, 3, 4, 5) is considered the same as (5,
4, 3, 2, 1) or (2, 1, 3, 4, 5). What's in it for you? The
5 best submissions will receive:
Solutions
I received a total of 9 submissions for this challenge (thanks
everyone!). It is quite a lot of work to describe them all in full
detail here, so I'll group them by technology used. I'll also announce a
group winner below.
Of course Excel has a function with which you can calculate the total
number of unique combinations:
=COMBIN(10,5)
which yields 252. That means that if a solution does not have 252
possible combinations the solution is (alas!) wrong.
Formula solutions
Three people submitted a solution involving formulas in Excel. Dan
Mayoh, Doug Jenkins and Richard Jubber. Two of them were correct and
both used a very similar approach to get the correct combinations.
Download the two correct formula solutions
Group winner
The best formula solution was provided by Dan Mayoh. Dan went out of
his way to deliver a nicely structured and formatted workbook which is
designed in such a way that you can add more draws if you like and even
change the number of available tickets. You do have to do some formula
copying if you want more than the default numbers, but the plumbing is
there.
Here is a screen-shot:
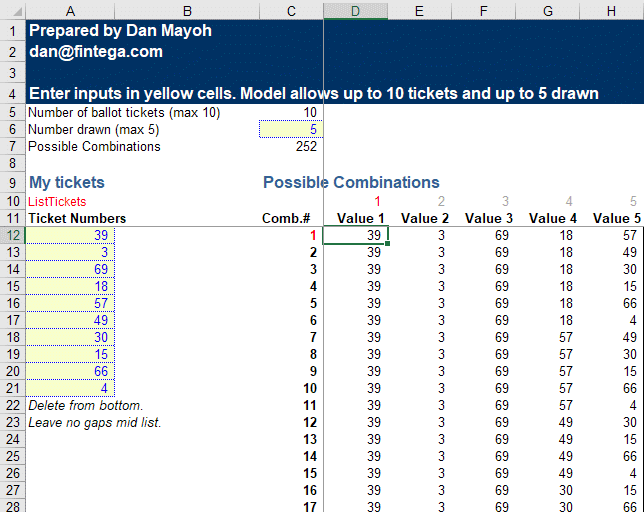
I plan to have an explanation here, which I'll ask Dan to write :-)
Runner-up in this category is Doug Jenkins. Doug also posted a VBA
solution for which he received some bonus points.
VBA Solutions
Four people submitted a solution using VBA: Harald Staff, Garys
Student, Doug Jenkins and Gerard Oudewaal. All four of them used very
similar techniques.
Download the VBA solutions
Group winner
The best VBA solution was provided by Harald Staff. Harald also
enables us to change the ticket numbers, though he did not go as far as
Dan so we cannot add more draws if we like or change the number of
available tickets.
Runner-up in this category is Garys Student (I already made Doug
runner up in the formula category, can't win twice!) and a nice third
place for Gerard Oudewaal.
PowerQuery solutions
Jeff Weir and Jonathan Cooper both posted a solution based on
PowerQuery, both using a similar technique using my aforementioned
newsletter article as its basis.
Download the PowerQuery solutionsGroup winner
I call it a draw. Jeff uses less queries in his solution, but
Jonathan's final query involves less steps.
And the overall winner is....
Dan Mayoh !
I've decided to provide all correct solutions with a free license for
my RefTreeAnalyser utility.
Congratulations to the winners, you'll receive your license as soon as
possible.
How to calculate the number of combinations
I asked the participants if they might explain the solution method
and I particularly liked this one from Harald Staff:
"Many years ago, I worked at a quiz show. One of the challenges was
to get seven questions, discard two, and answer the remaining five
correctly. The producer asked me how many possible combinations there
might be. I made this illustration for her:
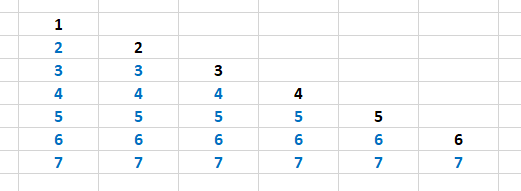
showing: 1 can only be combined with 2,3,4,5,6,7. 2 can be then only
be combined with 3,4,5,6,7 (1 has already been used with all other
numbers so no longer can be drawn). 3 can be combined with 4,5,6,7 (as
now 1 and 2 are off the table). And so on, summing up to 6+5+4+3+2+1=21
combinations. Your combinations challenge was very similar. Unique items
only once each, and the order of items does not matter. ABC and ACB are
the same.
My approach was also similar; work the table from the top and
downwards. To simplify the technique, here are five unique items, and
let us see how to find all the unique collections of three unique items.
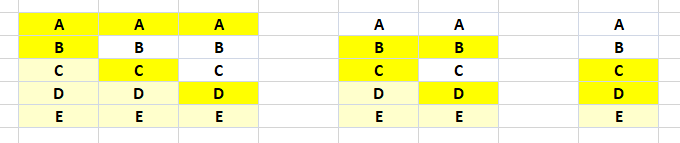
I use three loops for this. The outer loop controls the first item, A
at the beginning, the second loop controls the middle item, B at the
beginning, and the inner loop does the possible third items C, D and E.
So, we start on top, AB is combined with C, D and E. Now AB is done, we
move to AC, which is combined with D and E. Finally AD is combined with
E. Now we are done with A, the top item is now B. BC is combined with D
and E, and BD is combined with E. Done with B, our final starting point
is CD, which can only have E. Best wishes Harald"
