curves fitten met de kleinste kwadraten methode

Inhoud

• Inleiding
• Simpele lineaire vergelijkingen fitten
• Complexere functies fitten
• Uitleg bij het voorbeeldbestand
• Conclusie

Inleiding

Als je (net als ik, voordat ik Excel specialist werd) ingenieur bent, dan heb je waarschijnlijk het nodige aan experimenteerwerk gedaan. Vaak heb je dan een methode nodig om je meetresultaten te fitten met een kromme. En als je een echte ingenieur bent, dan heb je ook al een goed idee wat de soort vergelijking is die theoretisch bij je metingen zou moeten passen.

Misschien heb je wel metingen gedaan met resultaten zoals deze:

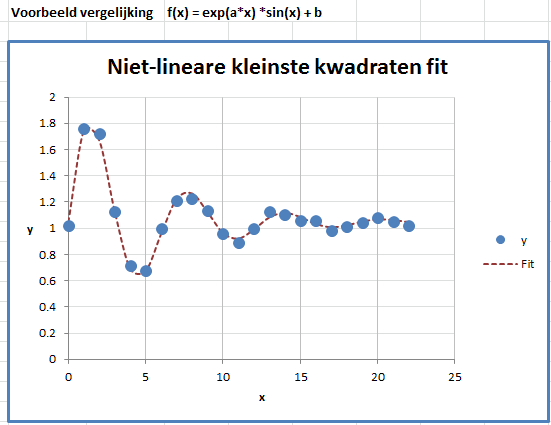
Gegevens fitten met een vergelijking.

Een zeer bekende methode om gegevens te fitten met een vergelijking is de methode der kleinste kwadraten (Least Squares). Ik ga hier niet de theorie uitleggen achter deze methode, lees daarover meer op de genoemde Wikipedia pagina.

Simpele lineaire vergelijkingen fitten

Excel bevat een aantal hulpmiddelen om berekeningen te doen met de kleinste kwadraten methode, maar deze beperken zich allemaal tot eenvoudigere (lineaire) functies in de vorm van:
y=a.x+b, y-a.exp(b.x), y=a.x^b etcetera. Met enkele trucjes kan je daarnaast ook polynomen fitten met Excel.

Regressie tools in de invoegtoepassing Analysis Toolpak

Activeer de Analysis Toolpak in je lijst met invoegtoepassingen (Bestand tab of Office knop, Excel Opties, tabje Invoegtoepassingen, klik Start):

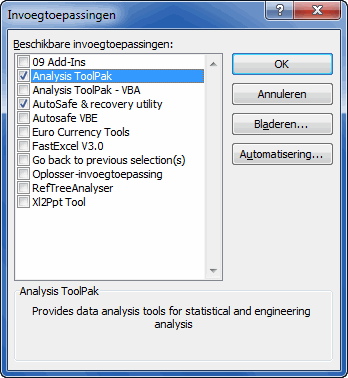
Excel's lijst met invoegtoepassingen met het Analysis toolpak geselecteerd

Hiermee wordt de groep "Analysis" aan je lint toegevoegd op de tab Gegevens met de knop Gegevens analyse (Dit is ook waar je straks de Oplosser knop kan vinden die ik verderop noem):

Lint met de groep Analysis (mijn Excel is een Engelse installatie met het Nederlandse taalpakket. Hierdoor worden sommige functies waaronder de invoegtoepassingen niet altijd volledig vertaald)

Klik op die knop om te zien welke regressie tools beschikbaar zijn.

Werkblad functies

Er is een aantal functies beschikbaar om regressie analyses mee te doen. Om deze snel te vinden druk je shift+F3 om de functie wizard te openen. In het zoekvak voer je in: "Regressie". Excel zal een aantal relevante functies tonen:

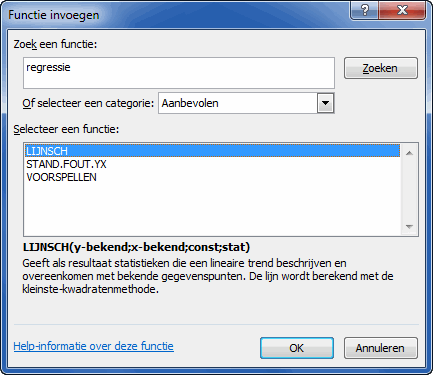
Functie wizard met Regressie functies

Helaas is deze lijst in een Nederlandse Excel niet compleet met deze zoekterm. Andere zoektermen zijn "Kleinste kwadraten" en "Fit". Kies er eentje uit en klik eens op Help-informatie over deze functie om er meer over te leren.

Complexere functies fitten

Wat nu als je een complexere functie hebt, zoals y=exp(a.x).sin(x) + b ? Hoe fit je deze curve met behulp van Excel?

Ik heb hiervoor een methode bedacht die de volgende stappen omvat:

• Maak een tabel met x en y waarden
• Voeg een kolom toe achter deze tabel met daarin de formule van jouw functie zoals je die in Excel moet invoegen, die verwijst naar je x-waarden en naar een paar cellen (met bereiknamen) die de constanten van de vergelijking bevatten die je wilt gaan schatten
• Voeg een kolom toe die de som der kwadraten berekent
• Gebruik Excel's Oplosser om de constanten te zoeken die de kleinste som der kwadraten vindt.

Uitleg bij het voorbeeldbestand

Ik heb een voorbeeldbestand gemaakt dat je direct kunt gebruiken. Hieronder vind je de link naar het bestand en een uitleg hoe dit bestand is samengesteld.

Download

Download dit bestand:

Non linear least squares

Hoe het bestand werkt

Gegevens

De gegevens en de calculatie staan beide op het werkblad Sheet1. het belangrijkste gebied is de tabel die start vanaf cel A1:

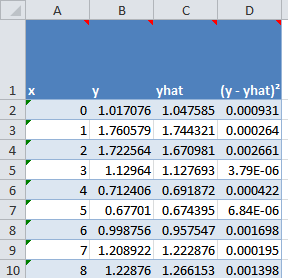
Data tabel in het voorbeeldbestand

Ik kolom A staan de x-waarden van de meting en in kolom B de gemeten waarden. De derde kolom bevat de vergelijking die gefit moet worden. Het voorbeeldbestand heeft deze vergelijking in kolom C:

=EXP(Const_a*xValues)*SIN(xValues)+Const_b

De vierde kolom berekent de kwadratische verschillen, formule:

=(B2-C2)^2

Zoals je waarschijnlijk al ziet heb ik gebruik gemaakt van enkele bereiknamen. Ik leg deze hieronder even uit.

Bereiknamen

Om het werken met het bestand eenvoudiger te maken heb ik bereiknamen toegepast. In plaats van te werken met de gestructureerde tabelverwijzingen heb ik in dit bestand gebruik gemaakt van dynamische bereiknamen. Tegenwoordig kunnen we de bereiknamen gewoon rechtstreeks laten verwijzen naar de cellen in de tabel omdat Excel er middels de tabelfunctionaliteit voor zorgt dat de bereiknamen worden aangepast als de tabel groeit of krimpt.

Constanten van de vergelijking

De bereiknamen die beginnen met "const" verwijzen naar een tweede tabel in het bestand:

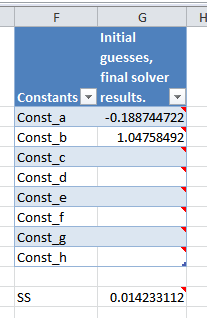
Constanten tabel

In deze tabel kan je je eerste schattingen ingeven voor de constanten. Hier zal de Oplosser bovendien de resultaten in plaatsen. Zoals je kunt zien is onder deze tabel de resterende som der kwadraten weergegeven. Formule:

=SOM(yDelta)

Het is deze cel die we met behulp van de oplosser invoegtoepassing gaan minimaliseren (kleinste kwadraten).

De oplosser gebruiken

Allereerst dien je de invoegtoepassing Oplosser te installeren, gebruik makend van het dialoogvenster invoegtoepassingen dat ik eerder al heb weergegeven. Zet een vinkje naast "Oplosser-invoegtoepassing", waarmee de knop "Oplosser" wordt toegevoegd aan de groep Analyse op de Gegevens tab in het lint.

Nadat je je ervan hebt vergewist dat je model formule in kolom C juist is ingevoerd en de berekeningen goed werken klik je op die knop. Het onderstaande venster opent (helaas heb ik daar de Nederlandse versie niet van):

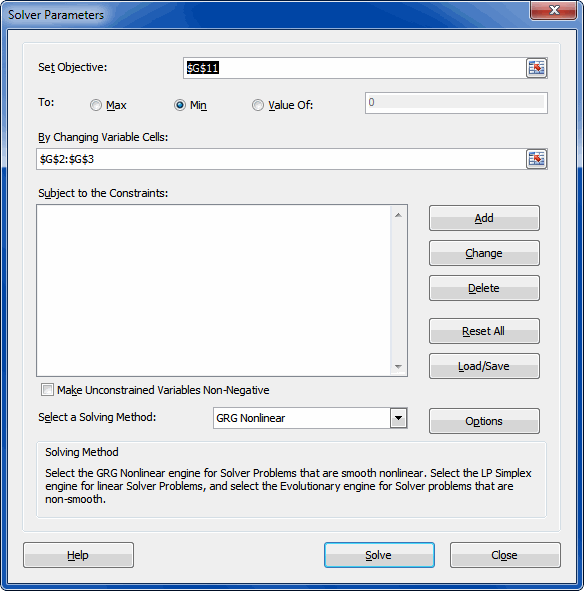
Het dialoogvenster van de Oplosser

Zorg ervoor dat het "Set Objective" vakje verwijst naar de cel met de som van de kwadratische verschillen. Selecteer "Min" bij "To".

Het vak "By Changing Variable cells" mag ALLEEN verwijzen naar cellen die ook echt in je model in gebruik zijn, anders klopt het aantal vrijheidsgraden niet dat wordt gebruikt bij de calculatie van de ANOVA (variantie analyse). Zorg er tevens voor dat de cellen van de niet gebruikte constanten leeg zijn door ze aan te klikken en op de Del toets te drukken.

Merk op dat je afhankelijk van je model soort mogelijk de instellingen van Oplosser moet aanpassen. Het kan hier nodig zijn wat met die instellingen te experimenteren voor het beste resultaat. Je kunt instellingen opslaan en openen met de betreffende knoppen van de oplosser.

Wees dus verstandig en kritisch en bekijk goed of de gevonden oplossing daadwerkelijk een juiste fit van je gegevens is want de Oplosser komt niet altijd met het beste resultaat. Wat het resultaat is hangt soms sterk af van de gekozen instellingen van de oplosser.

Als je tevreden bent met de huidige instellingen van de oplosser klik je op "Solve" (Oplossen?). Als vervolgens na enige tijd het dialoogvenster Oplosser resultaten opent, dan krijg je enkele opties om verder te gaan. Merk op dat je hier ook enkele keuzemogelijkheden krijgt voor het genereren van een rapport.

Het eindresultaat in het voorbeeldbestand is:

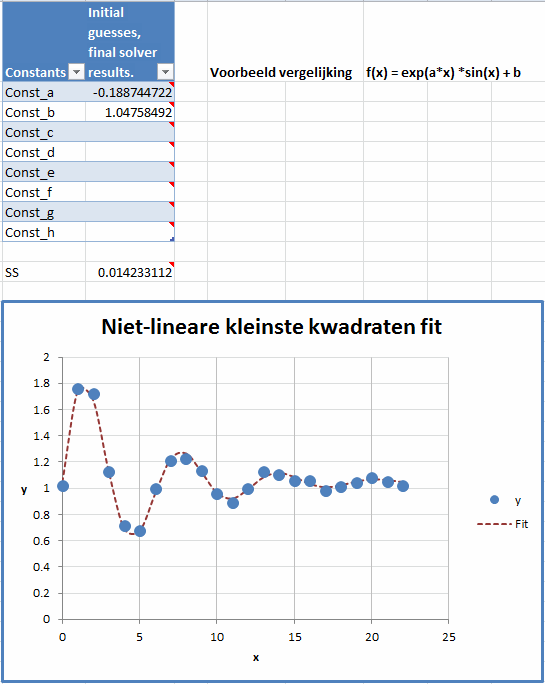
Het eindresultaat

Variantie analyse

Op het werkblad ANOVA, vind je de Variantie analyse, die er zo uitziet:

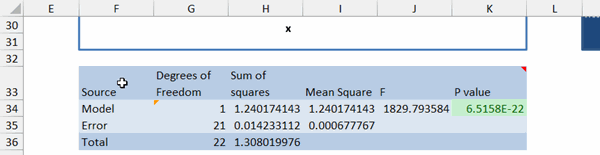
De ANOVA tabel

De belangrijkste cel van deze tabel is cel K34. Zolang de waarde van deze cel kleiner is dan 0,05, dan is er een waarschijnlijkheid van 95% dat je model je data correct fit. Dus "less is more" voor deze cel, de waarde ervan moet onder de 0,05 blijven. Met hulp van voorwaardelijke opmaak wordt deze cel rood bij waarden boven de 0,05.

Controleer wel even of de waarde in cel G34 exact 1 minder is dan het aantal constanten in je model. Dus gebruik je alleen de constanten const_a en const_b, dan moet er in cel G34 1 staan (model degrees of freedom).

Conclusie

Zoals je ziet is het fitten van complexe functies niet heel moeilijk om te doen als je van de genoemde trucjes gebruik maakt. Een combinatie van enkele relatief eenvoudige formules en de Oplosser invoegtoepassing schieten je hier te hulp.

Tot slot nog een advies van de ene ingenieur aan de andere: Wees alsjeblieft kritisch. Geloof niet alles wat Excel je vertelt. Analyseer het resultaat nauwgezet want de oplosser geeft wel eens onjuiste resultaten en dus niet de juiste oplossing van je probleem!